The Importance of Choosing the Right Sample Size for Trial Assessment
Thu Oct 24 2024
Author
Wilan Wong
A critical process in utilising AI/ML and any data driven solution is to assess the effectiveness of impacted decision making processes in production. For this assessment to happen, we need to carefully define trials that can statistically validate any differences between using an AI/ML solution and one that does not.
One of the commonly asked questions that precedes this trial creation process is “What sample size do I need to validate any observed effect from my intervention?”.
In general for hypothesis testing, the sample size is crucial for obtaining reliable and robust results. In this article, we shed light on why sample size is important to get correct, and what are some of the factors that influence the sample size we need to obtain from different groups (i.e., treatment and control groups). We will finish off with a technical deep dive into how one would calculate the right sample size for trial assessment.
But first, let’s walk through what is “hypothesis testing” and how sample size comes into play.
What is “Hypothesis Testing”?
Hypothesis testing is a statistical method used to make inferences or draw conclusions about a cohort based on sample data. In this process, we formulate hypotheses and then test whether the sample data provides enough evidence to reject the null hypothesis.
We typically formulate a null hypothesis which is a statement saying that there is no effect or no difference. This largely serves as a default or baseline assumption. In the context of crafting a trial - this is synonymous to saying that the intervention of utilising data-driven insights yields no benefits over not utilising.
To test if this is true, we divide our population into two groups - one for control and one for treatment. The control group is a cohort in which they do not receive any intervention. The treatment group is a cohort in which they do. We can then quantify the differences between these two groups to see if there is indeed an uplift.
How does sample size come into the picture?
The sample size refers to the number of individual observations or data points included in a statistical sample. It is the subset of a population that is selected for a particular study or experiment to represent the entire population.
The sample size directly influences our ability to detect a true effect if it exists. To detect if there is an effect from the intervention, we need to sample from the overall population. An instance of a sample could range from specific retail customers to a vending machine. The number of samples we put into each group allows us to statistically argue for observed effects.
To make this concrete, let’s say for example, we were looking to see if an assortment optimisation methodology works for a retailer. Let’s assume we have 1000 stores - we can divide up these stores and place them in either the treatment group (for the stores to utilise the optimisation strategy) or place them in the control group (we keep them like status quo).
It may not make practical sense to utilise the entire fleet of stores for the trial. We effectively want to assess the effect whilst using the least amount of stores whilst maintaining statistical validity. Some reasoning behind this:
- It can be prohibitively expensive to roll out changes to all stores
- We do not understand if the change is a good one - if we inadvertently a poor optimization methodology to many stores - then there would be a huge operational cost to the business
- There are diminishing returns (in terms of statistical inference) to gathering more samples over a certain threshold which means the insights you get become disproportionately worse
On the other hand, if we chose too few stores - say we chose a single store for the treatment and a single store for the control group. It is unrealistic to generalise the insights to all the 1000 stores just from these two samples. In this case, we cannot rely on the results as the difference in performance for these stores is likely due to noise.
As with all things - there is a trade-off between using too few and too many samples. Hence, being able to efficiently determine the right sample size is an important step to creating and evaluating our trial and its results.
Striking the right balance
To delve further into determining the right sample size, we need to understand what influences the sample size required.
Some of the key factors which are all inter-related are:
- Effect size: Effect size refers to the magnitude of the difference we are testing for. If it exceeds this magnitude of difference, then we consider the intervention having an effect. Larger effect sizes generally require smaller sample sizes to detect a given effect with the same level of confidence. Conversely, smaller effect sizes require larger sample sizes to reliably detect the effect. Our ability to detect a particular effect size is also affected by the variance (or standard deviation) of the effect we are trying to measure. For example, if the stores have wildly different performance in the same group - we would need more samples to account for this variation.
- Statistical Significance: Statistical significance is the likelihood that the observed results are not due to chance. The significance level (often denoted as alpha α) represents the threshold for rejecting the null hypothesis (as stated above). A lower significance level (i.e., 0.05 instead of 0.1) means we require stronger evidence to reject the null hypothesis - this typically equates to requiring a larger sample size. Basically, we need more samples to be more confident about our statistical results. This relates to Type 1 errors - essentially rejecting the null hypothesis when there are no effects (thinking there is an effect but there is none in reality).
- Statistical Power: Statistical power is the probability of correctly rejecting the null hypothesis when it is false (i.e., detecting a true effect). Higher power (typically 80% - 90%) requires a larger sample size because it means you’re aiming to correctly detect effects with greater certainty. This relates to Type 2 errors (typically denoted as beta β) - where β refers to the probability of not rejecting the null hypothesis when there is an actual effect. Statistical power is the inverse of this, power = 1 - β. So the higher the power the better (conversely, the lower the β the better).
These factors and the relationship to sample size can be summarised in the table below:
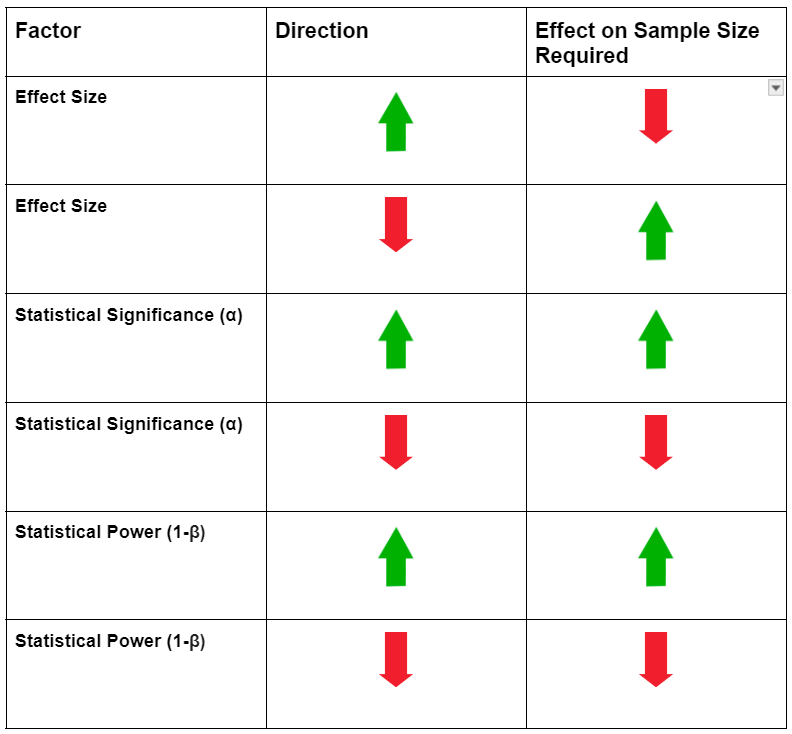
Once we understand how each factor influences the sample size required - we can develop some intuition on when to increase / decrease the sample size based on our requirements or scenario.
Next, we quantify how this would work mathematically by using a technique called power analysis.
Determining the right sample size
Power analysis is an effective way to help determine the minimum sample size required to detect an effect of a given size with a specified level of confidence. Within power analysis, there are different variations used to determine the right sample size. This largely depends on the specific situation - such as whether or not the two groups (treatment and control) have the same number of samples as well as the type of effect we are measuring (continuous or dichotomous) amongst other factors.
We will keep it simple and look at the case where the two groups should have the same number of samples and we are measuring the mean difference between these two groups. The mean in this case could be the mean of the observed sales in each group.
One way to understand how power analysis works is by visualisation.
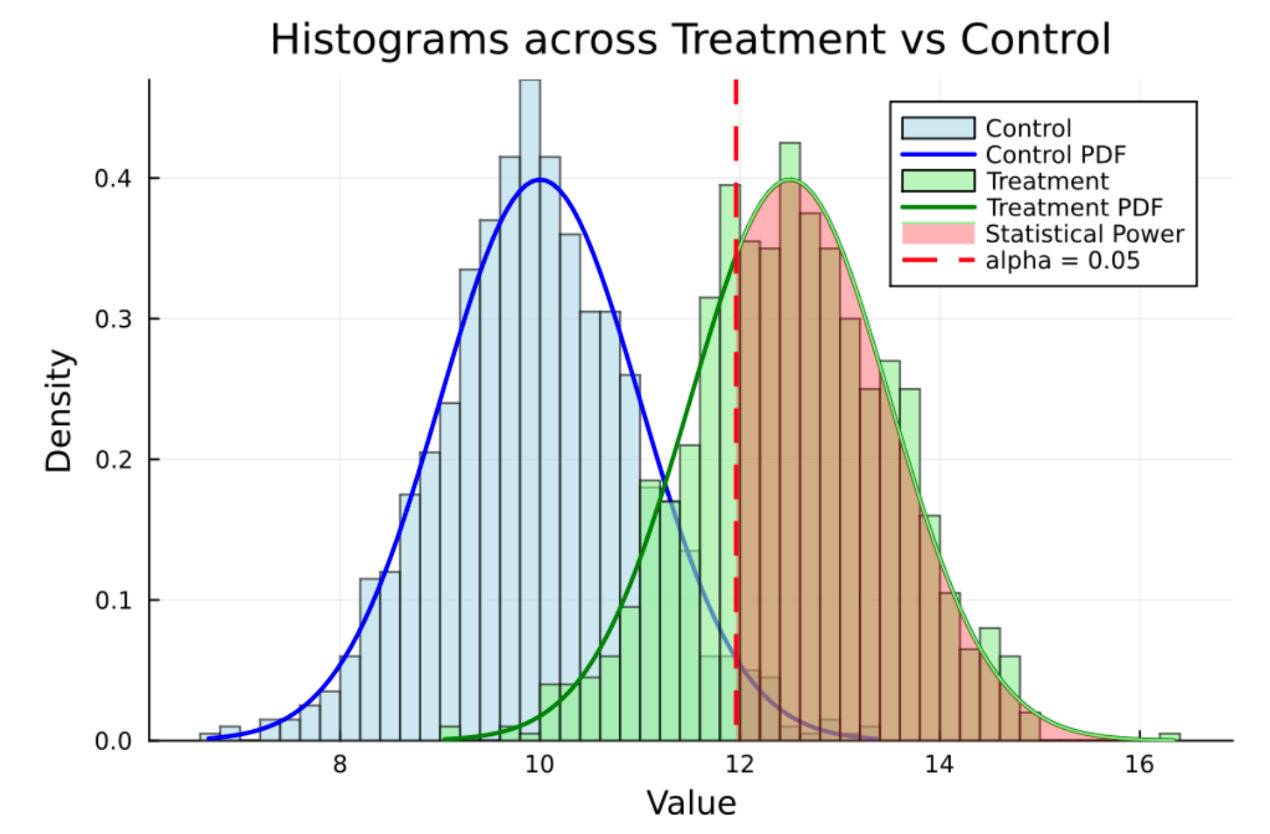
We can see two distributions - the blue histogram denotes the control group, the green histogram denotes the treatment group. It’s clear visually there is an overall effect of the intervention even though there is an overlap between the 2 distributions.
The red dotted line represents the cut-off point for alpha = 0.05 (2 tailed), so this represents the 0.975 quantile value for the control group. The statistical power is the shaded area or portion of the treatment distribution that is greater than this alpha value.
Statistical power is the overlap between the two distributions. We can achieve greater statistical power by increasing the alpha level (i.e., from alpha = 0.05 to 0.1), this makes it easier to reject the null hypothesis thus increasing power. The trade-off is that this increases the risk of a Type 1 error - so you need to carefully balance this risk against the gain in statistical power. You can view this in the diagram above - if the alpha = 0.05 was larger, the red line would shift to the left which would mean the shaded area (in red) would increase. There are other ways to increase statistical power such as increasing sample size or increasing the effect size.
This creates stronger evidence that the 2 distributions are different and hence more evidence for us to reject the null hypothesis that the 2 distributions are the same (i.e., the intervention had no effect for the treatment group).
If we look mathematically, the optimal sample size is derived as:
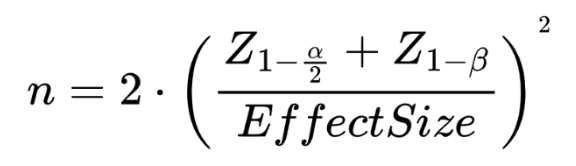
Where:
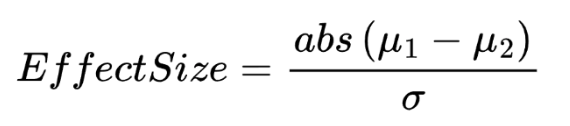
The important takeaways is:
- We need to supply several parameters such as:
- If the σ goes up, this has asquaredeffect on the minimum sample size required. For example, if σ goes up by a factor of 2 - the minimum sample size required goes up by 4 for everything else kept constant
- If there is only a small difference between the two groups, the effect size becomes small which means you need a much larger sample size to get the same statistical validity
- We need to jointly consider good levels for both α and statistical power (1-β) to get a good test
- It pays to be conservative in our estimations - generally for most cases it’s better to have a slightly higher sample size than an underestimation
- The formula also affirms the relationships between the factors we discussed in the last section
- The value ofnmay not be an integer - we should take the floor (round up to the nearest integer) of the real number as the minimum sample size (this also follows the same principle of being conservative in our estimations)
Implementing a simple function that computes the minimal sample size
We can encapsulate the logic quite easily using any programming language that has easy access to basic statistical functions. We have chosen to demonstrate how you could implement the logic above using Julia:
function calculate_sample_size(alpha, beta, effect_size) return 2 * ((quantile(Normal(0, 1), 1 - (alpha / 2)) + quantile(Normal(0, 1), 1 - beta)) / effect_size)^2 end
Then to test this functionality out - we can choose an alpha = 0.05, beta = 0.2 and effect_size = 0.1. This gives an output of:

Which means for these parameters, we need a minimum of 393 samples in each group. Totalling 786 across both treatment and control group. Note that we can relax the conditions of having equal samples for each group - although this would require some minor modifications to the methodology shown above.
Wrapping up
We hope that this article provides you with some insight into the process of choosing a sample size that can statistically measure the desired effect. Note that we have only scratched the surface - there are many variations and assumptions you can make that would change the way you would determine the optimal sample size number. Choosing the right sample size is an important first step in establishing a trial to assess the impacts of data-driven decision making. There are still many other steps that are required to go from trial ideation, creation and finally to trial measurement and continuous improvement.
As part of our jahan.ai platform, we have embedded and integrated these computations into an easy to use interface that allows usability whilst maintaining the rigour required for the end-to-end trial creation and measurement workflow. If you would like to know more - reach out through our contact information provided below.
#abtesting #trialandlearn #testandlearn #ai #datascience #businessexperimentation #jahanai #samplesize
At jahan.ai, we build end-to-end AI twins for retail and supply chain businesses. We take the concept of a digital twin, a virtual replica of business processes, further with advanced AI, which not only mirrors these processes but also automatically optimises them. In this way, we support businesses in driving efficiency, going beyond their potential.